What Is Big O Notation?
In this article, take a look at a short guide to get to know Big O Notation and its usages.
Join the DZone community and get the full member experience.
Join For FreeAs programmers, we often find ourselves asking the same two questions over and over again:
- How much time does this algorithm need to complete?
- How much space does this algorithm need for computing?
To put it in other words, in computer programming, there are often multiple ways to solve a problem, so
- How do we know which solution is the right one?
- How do we compare one algorithm against another?
The big picture is that we are trying to compare how quickly the runtime of algorithms grows with respect to the size of their input. We think of the runtime of an algorithm as a function of the size of the input, where the output is how much work is required to run the algorithm.
To answer those questions, we come up with a concept called Big O notation.
- Big O describes how the time is taken, or memory is used, by a program scales with the amount of data it has to work on
- Big O notation gives us an upper bound of the complexity in the worst case, helping us to quantify performance as the input size becomes arbitrarily large
- In short, Big O notation helps us to measure the scalability of our code
Time and Space Complexity
When talking about Big O Notation it’s important that we understand the concepts of time and space complexity, mainly because Big O Notation is a way to indicate complexities.
Complexity is an approximate measurement of how efficient (or how fast) an algorithm is and it’s associated with every algorithm we develop. This is something all developers have to be aware of. There are 2 kinds of complexities: time complexity and space complexity. Time and space complexities are approximations of how much time and space an algorithm will take to process certain inputs respectively.
Typically, there are three tiers to solve for (best case scenario, average-case scenario, and worst-case scenario) which are known as asymptotic notations. These notations allow us to answer questions such as: Does the algorithm suddenly become incredibly slow when the input size grows? Does it mostly maintain its fast run time performance as the input size increases?
Best case — being represented as Big Omega – Ω(n)
- Big-Omega, written as Ω, is an Asymptotic Notation for the best case, or a floor growth rate for a given function. It gives us an asymptotic lower bound for the growth rate of the runtime of an algorithm.
Average case — being represented as Big Theta – Θ(n)
- Theta, written as Θ, is an Asymptotic Notation to denote the asymptotically tight bound on the growth rate of the runtime of an algorithm.
Worst case — being represented as Big O Notation – O(n)
- Big-O, written as O, is an Asymptotic Notation for the worst case, or ceiling of growth for a given function. It gives us an asymptotic upper bound for the growth rate of the runtime of an algorithm.
Programmers typically solve for the worst-case scenario, Big O
Because we are not expecting our algorithm to run in the best or even average cases.
How to Calculate Big O of an Algorithm
Suppose we want to write a function that calculates the sum of all numbers from 1 up to (and including) some number n

Question: How do we know which one is better? Can we use time to measure it?
Answer: The problem with time is that different machines will record different times. The same machine will sometimes record different times. For fast algorithms, speed measurements may not be precise enough.
Question: If not time, then what?
Answer: Rather than counting seconds, which are so variable. Let’s count the number of simple operations the computer has to perform.

This function will take 3 simple operations, regardless of the size of n. If we compare to the below function, we have a loop and it depends on the value of n.

We can see that as n grows towards some large number approaching infinity, the number of operations that we have to do will also grow at least in proportion with n.
Here are 4 rules to find the Big O complexity of an algorithm
- Rule 1: Worst case
- Rule 2: Remove the leading constants
- Rule 3: Different terms for inputs
- Rule 4: Drop nondominanthttps://medium.com/@dsvgroup/what-is-big-o-notation-15b20ed7d6f1?sk=c0627471015259ff6a9dd5f701aacace terms
Apply those rules for our 2 examples above, the Big O complexity of them are O(n) and O(1) respectively.
Another example: Find Big O complexity of an algorithm with the time complexity 20n³ + 5n + 7?
Using the rules, this can be simplified to O(n³).
Big O Complexity Chart
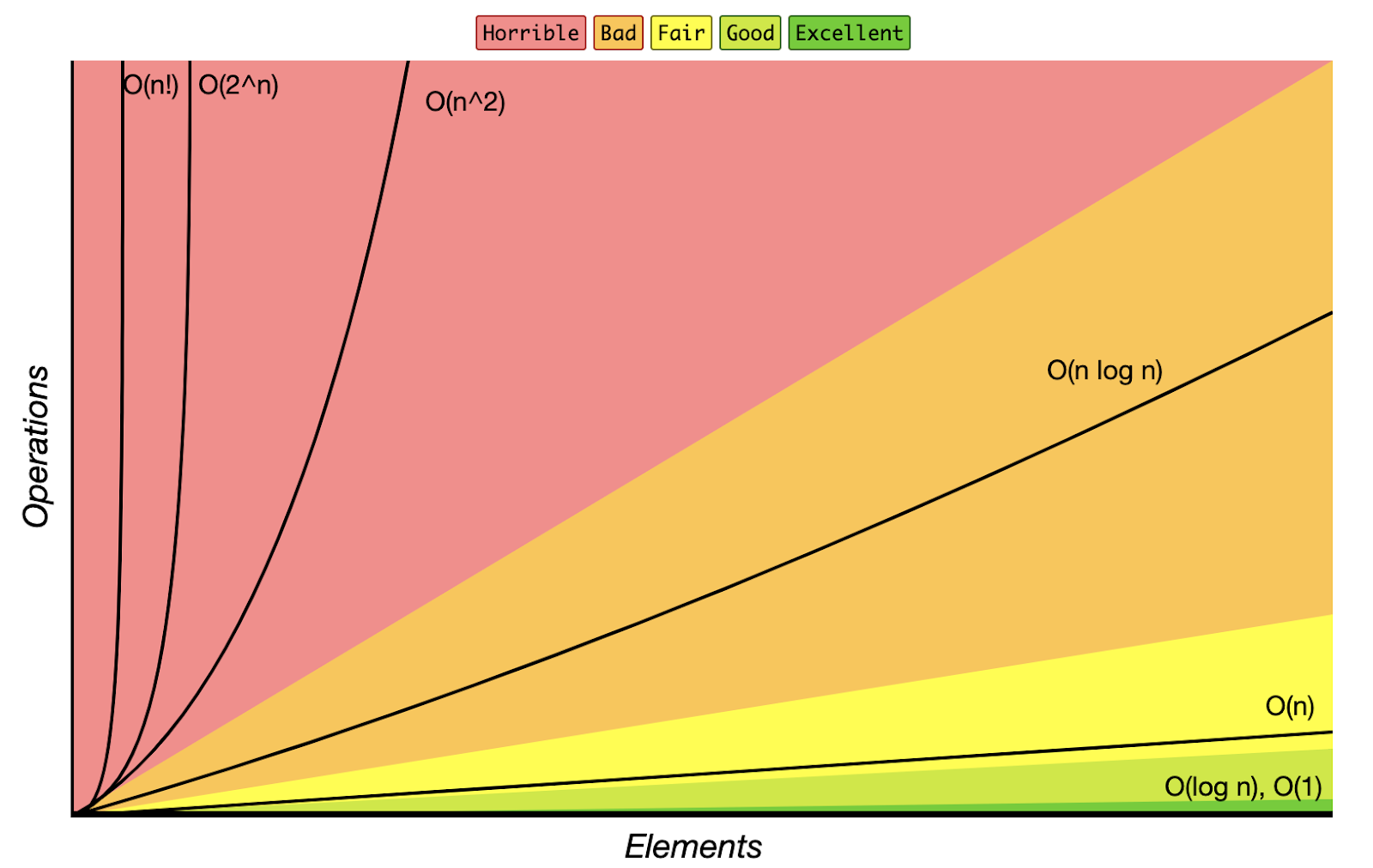
When talking about scalability, programmers worry about large inputs (what does the end of the chart look like). When writing code, we tend to think in here and now. For example, we think that our website or our app will only have a few hundred users and that’s it. If we know our input is going to be small (ex: an array of 5 items), Big O won’t matter as much. But what if that user base grows, what if our inputs grow? We never know that.
In real-life scenarios, we want to write code that can scale, so we don’t have to go back and fix things or when it gets out of hand, the code won’t break. The Big O chart helps us to think about our code/algorithms in the long-term and think about what could happen in the future.
Cheatsheets
- O(1) Constant- no loops
- O(log N) Logarithmic- normally searching algorithms have log n if the input is sorted (Binary Search)
- O(n) Linear- for loops, while loops through n items
- O(n log(n)) Log-Linear – usually sorting operations
- O(n^2) Quadratic- every element in a collection needs to be compared to every other element. Two nested loops
- O(2^n) Exponential- recursive algorithms that solve the problem of size N
- O(n!) Factorial- we are adding a loop for every element
- Iterating through half a collection is still O(n)
- Two separate collections: O(a * b)
That’s all. We hope that this article has provided some useful information about Big O Notation for you! Cheers!
Published at DZone with permission of Huyen Pham. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments